Podríem dir que aquesta necessitat de fer matemàtiques comença quan els humans vam començar a viure en societat. O potser més acuradament, quan vam sentir la necessitat de comptar. Però quan es comença a fer matemàtiques com les entenem avui?
Comptant el bestiar
Al principi, els humans fèiem agrupacions per tal de saber quin dels conjunts comptava amb més elements. Així, deixant al matí tantes pedres com ovelles sortien a pasturar, els pastors eren capaços de saber si totes les ovelles havien tornat al vespre; només havien de tornar-les a emparellar. Tot això ho feien sense necessitar números. D’una forma anàloga, els matemàtics actuals utilitzen aquesta tècnica per desvelar els secrets de l’infinit.
A part, de seguida van començar a veure que podien anotar aquests comptes per deixar-ne una constància duradora: fa més de 20000 anys, molt abans de desenvolupar la primera escriptura, trobem un os amb 28 marques.

Però això, ja són matemàtiques? Quan podem dir que neixen? O, en definitiva, què entenem per matemàtiques en l’actualitat? Aquesta és una pregunta molt complexa que segurament es pot respondre de maneres molt diferents…
Primeres mostres de matemàtiques
En les primeres civilitzacions urbanes —per exemple a Mesopotàmia i Egipte—, ja trobem senyals de càlculs matemàtics. Els mesopotamis van viure entre el Tigris i l’Eufrates al voltant del 3500 aC, a l’actual Iraq i parts de Síria, Iran i Turquia. Van desenvolupar un fort coneixement científic, des de l’arquitectura fins a l’astronomia.
Cap a l’any 3000 aC, els sumeris van crear l’escriptura cuneïforme a través de la impressió que deixava una canya de fang —amb l’extrem amb forma de falca— a una tauleta d’argila. Algunes d’aquestes tauletes varen quedar enterrades i se n’han pogut recuperar centenars de milers, de les quals, al voltant de 100 contenen raonaments matemàtics.
Els babilonis, per la seva banda, feien servir un sistema numèric posicional —com el nostre— en base 60. Això vol dir que tenien 60 símbols pels primers 60 números i després saltaven una posició a l’esquerra. Nosaltres fem el mateix però amb 10 símbols. Quan arribem al 9, obrim una nova posició i tornem al zero a la primera: 10. Aquest sistema posicional és bastant pràctic i ha perdurat fins ara, a diferència d’altres com el dels romans, que per escriure números grans necessita crear nous símbols.
Una bona pregunta que ens podem fer és: perquè 60? En el nostre cas, justificar el 10 és més fàcil: tenim 10 dits a les mans. Una de les hipòtesis és perquè el seixanta té molts divisors i, per tant, és molt més fàcil calcular-hi.
Plimpton 322
En qualsevol cas, una de les tauletes més famoses de matemàtiques que s’han recuperat és la Plimton 322. Aquesta tauleta conté ternes pitagòriques, és a dir, nombres enters que satisfan que la suma dels quadrats de dos d’ells és el quadrat del tercer.
![]()
La datem entre 1790 i 1750 aC, més de mil anys abans que Pitàgores postulés el seu teorema.

Hi ha dues hipòtesis principals sobre l’ús d’aquesta tauleta. Alguns historiadors argumenten que era una tauleta pedagògica: servia a un professor per posar problemes de triangles rectangles als seus alumnes. Altres opinen que era una tauleta de caràcter pràctic, una taula de dades: quan necessitaven resoldre la longitud d’alguna de les arestes d’un triangle rectangle, la podien consultar.
Aleshores, podem dir que aquesta tauleta són matemàtiques tal com ara les coneixem, amb teoremes, demostracions, justificacions… o és només una eina de càlcul? Amb aquesta tauleta podem dir que els mesopotamis entenien i construïen la ciència tal com ho fem ara?
L’axiomàtica grega
Segurament podríem estar d’acord que van ser els grecs —i en concret Euclides— els que van assentar les bases de les matemàtiques com les entenem avui. Euclides va decidir exposar tot de problemes geomètrics —molts dels quals ja havien tractat amb anterioritat altres civilitzacions com l’egípcia o la mesopotàmica— però de forma completament rigorosa.
Va partir d’uns postulats o certeses que prenem a priori, i d’algunes definicions. Utilitzant únicament aquests postulats o axiomes es va dedicar a combinar les definicions fins a tenir resultats matemàtics. Així, va fer una demostració tal com l’entenem ara. Tot això ho va deixar recollit als 13 llibres que va publicar amb el títol d’Els Elements, al segle III aC.
Euclides va definir les nocions de punt, línia, segment, circumferència, etc. —tal com ho definiríem avui— i va establir els 5 postulats següents:
| D’un punt a un altre es pot tirar un segment rectilini [únic] |
| I prolongar-lo de forma contínua amb una recta limitada |
| Per a cada centre i distància es pot descriure un cercle |
| Tots els angles rectes són iguals entre si |
| Per un punt que no pertany a una recta hi passa una única paral·lela a la recta |
Una demostració!
Combinant aquests postulats, va crear nous teoremes. Així, el primer teorema que demostra a Els Elements és el següent:
Volem construir un triangle equilàter sobre un segment rectilini donat
Elements 1-1
És a dir, donat un segment, volem demostrar que només usant els postulats podem construir un triangle que tingui els tres costats iguals —on un dels costats és el segment inicial. És interessant seguir la demostració que fa:
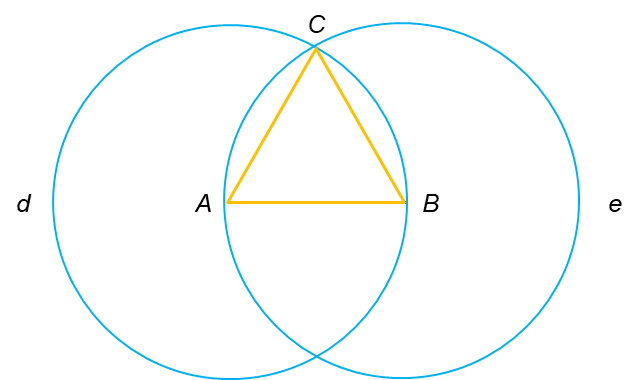
- Suposem que el segment donat és l’AB de la figura anterior.
- Utilitzant el 3r postulat podem construir dues circumferències de centre A i B respectivament amb radi AB. Les anomenarem d i e, respectivament.
- Unim el punt on es tallen les dues circumferències (C) i tenim els segments AC I BC. Queda veure que aquests segments són iguals a l’AB.
- Com que A és el centre de la circumferència d, tots els punts que estiguin en ella estaran a la mateixa distància —per la definició de circumferència. Així, el segment AB i AC seran iguals.
- Anàlogament, per la circumferència e, els segments AB i BC seran iguals.
- Per tant, hem conclòs que els segments AB, AC i BC són iguals, demostrant que podem construir un triangle equilàter donat un segment. Tal com volíem veure.
D’aquesta forma tan pautada, Euclides enuncia 465 proposicions en els 13 llibres que componen Els Elements. Algunes de molt més complexes, com per exemple que hi ha infinits nombres primers. Així, s’assegura que tot el que fa està fonamentat i justificat, és a dir, que serà sempre cert si partim dels mateixos postulats.
Aquest ànim demostratiu és el que ha caracteritzat les matemàtiques fins a l’actualitat. No ens serveix enunciar un resultat que sembli evident i prou: cal anar més enllà i justificar, partint de les idees més bàsiques, que el resultat és cert. D’aquesta forma, és com sorgeixen les matemàtiques.
Ja per acabar…
A principis del segle XX, les matemàtiques van patir una crisi de fonaments. Es van tornar a revisar tots els axiomes i postulats sobre els quals es basaven les diferents disciplines. Un dels principals instigadors d’aquesta revisió va ser el matemàtic David Hilbert, que va completar els axiomes d’Euclides. Hilbert es va adonar que en la demostració anterior no l’hem justificat de cap manera si el punt C realment existeix. No hi ha cap postulat ni definició que ens garanteixi que efectivament el punt és allà.
Aquesta crisi va portar a fer un estudi profund a com estaven construïdes les matemàtiques, i va arribar a un resultat sorprenent: en qualsevol sistema d’axiomes on es pugui fer aritmètica bàsica hi haurà proposicions que no es podran demostrar ni refutar. Això, però, ho deixem per un altre reportatge.
Per saber-ne més
Byrne’s Euclid – The Elements of Euclid With Coloured Diagrams and Symbols
History of Mathematics Project – Plimton 322
Cuaderno de la Cultura Científica – El origen de la escritura de los números
Imatges extretes de:
1. Wikimedia Commons