Fa uns anys, una notícia científica va irrompre a tots els mitjans de comunicació del món: un grup interdisciplinari de científics espanyols havien descobert una nova figura geomètrica. Es deia que tot plegat tenia a veure amb un problema d’empaquetament cel·lular. Però, què hi tenen a veure les cèl·lules en el descobriment d’aquesta nova figura? 

Aquesta descoberta sorprenent va involucrar una gran feina de col·laboració entre la biologia, les ciències computacionals, les matemàtiques i la física! Tot va començar quan estaven estudiant com s’organitzaven les cèl·lules en uns teixits molt concrets: els epitelials. Comencem per aquí!

Els teixits epitelials

El nostre organisme està format per cèl·lules, i aquestes s’organitzen en forma de teixits cel·lulars. N’hi ha de diferents tipus: el teixit muscular –propi dels músculs–, el teixit ossi –que forma els ossos– o el teixit neuronal –del sistema nerviós–, entre d’altres. Segons la funció que facin, uns teixits tindran unes característiques o unes altres. Així, per exemple, les cèl·lules de la sang han de poder moure’s àgilment pels vasos sanguinis i les dels músculs han de poder fer força les unes amb les altres.

Avui, però, ens fixarem en un tipus de teixit concret: l’epitelial. Aquestes cèl·lules són les encarregades de recobrir les superfícies, cavitats i òrgans del cos. La pell és l’exemple per excel·lència de teixit epitelial, però també el podem trobar recobrint les vies respiratòries, l’esòfag, l’estómac, els intestins, l’aparell urinari i un llarg etcètera. Aquestes cèl·lules tenen una funció protectora, de relació entre diferents teixits i de transport de substàncies. 

Per aquest motiu, la propietat més important d’aquest teixit és que les cèl·lules estiguin ben empaquetades, amb ben poc espai intracel·lular. Ens podem imaginar els teixits epitelials com capes de cèl·lules ben compactades.

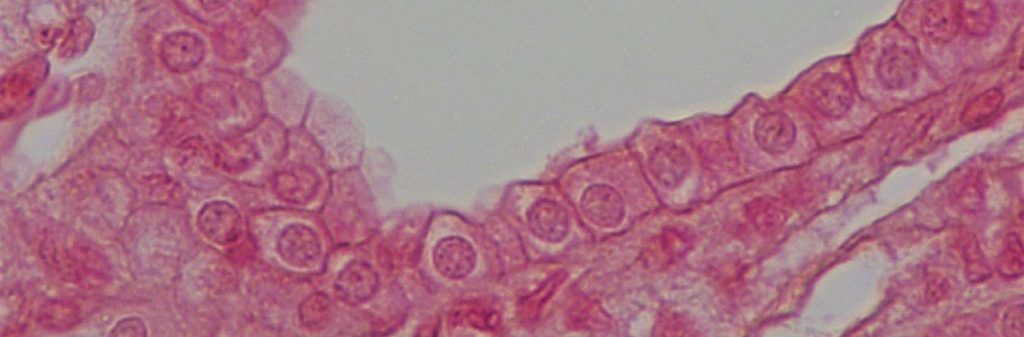
1. Els teixits epitelials formes capes de cèl·lules ben empaquetades

Aquesta propietat obre una pregunta interessant: quines formes prenen aquestes cèl·lules per poder ocupar tot l’espai del qual disposen?

Idea inicial

Abans de la publicació de l’article en el qual en centrem avui existia un model clàssic. Aquest model descrivia les cèl·lules en forma de prismes i així aconseguia explicar aquest empaquetament tan característic del teixit epitelial.

Quan ens mirem la capa des de dalt, amb un microscopi, veiem que les cèl·lules prenen formes hexagonals o pentagonals, igual que un rusc d’abelles. Així, sembla lògic descriure el teixit com un conjunt de prismes. Però què passa si el teixit en qüestió té una certa curvatura? Doncs llavors el podem modelitzar amb un tronc, o cosa que és el mateix, amb una piràmide tallada. Ho podem veure al dibuix següent:

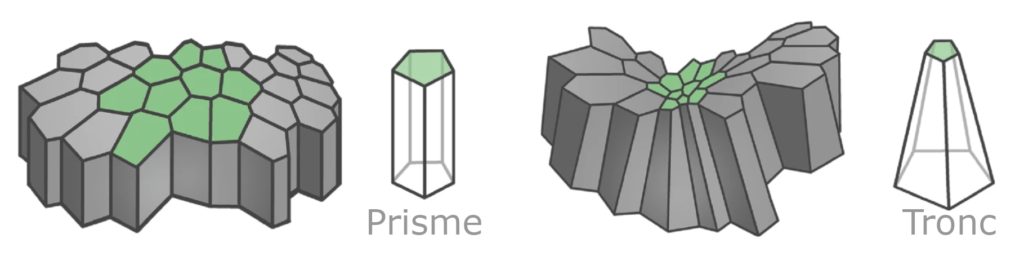
2. Modelitzem una capa de teixit epitelial com un conjunt de prismes. Si hi ha curvatura, fem servir troncs.

Però això no ens acaba de servir…

Els autors d’aquest estudi van fer créixer al laboratori teixit epitelial d’una sola capa de cèl·lules recobrint un cilindre –una superfície corbada– i van observar un fet que no podien descriure amb el model anterior: van veure que hi havia conjunts de quatre cèl·lules que s’intercanviaven els veïns entre les dues superfícies del cilindre. Així, dues d’elles estaven en contacte a la superfície interior, separant les altres dues, mentre que a la superfície exterior era exactament al revés: les cèl·lules que eren veïnes ara no estaven en contacte, i les altres dues en aquest costat es tocaven. Segurament en l’esquema següent queda molt més clar:

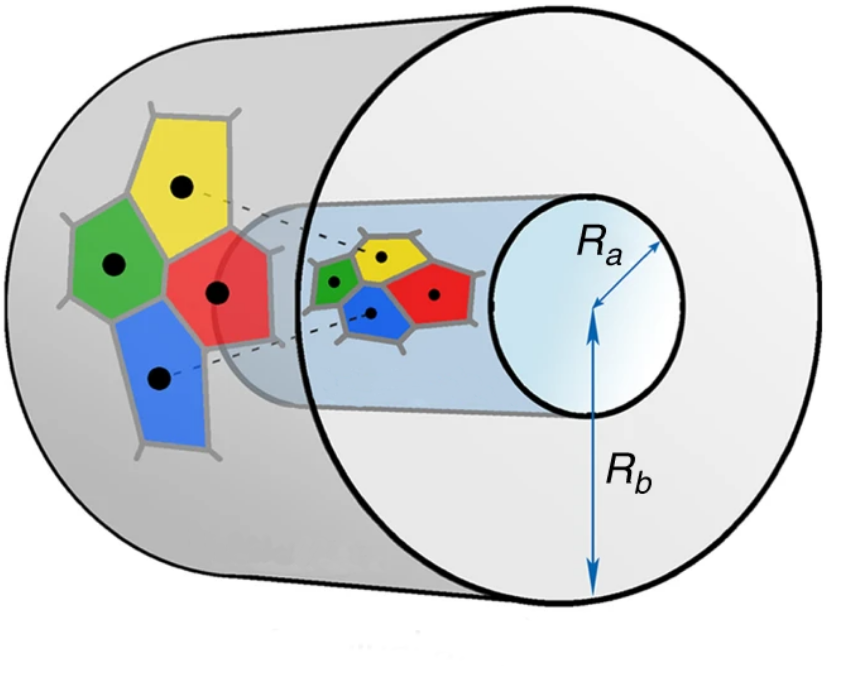
3. Esquema del que observaven al microscopi en fer créixer cèl·lules epitelials en un cilindre. Només està representat la capa superior i inferior de la cèl·lula, és a dir, els mateixos colors corresponen a la mateixa cèl·lula. En aquest cas, les cèl·lules vermella i verda són veïnes a la superfície superior mentre que a la superfície inferior ho són la groga i la blava.

Aquest fet no es pot descriure utilitzant prismes i troncs com fèiem fins ara i, per tant, calia un nou model.

Un nou model

Aquí va ser quan van entrar els investigadors en ciències de la computació, matemàtics i físics i van formular un nou model que descrivia aquests canvis de veïns observats al laboratori. Per fer-ho, van utilitzar el que s’anomena diagrames de Voronoi.

Aquesta tècnica consisteix a dividir un espai de dues dimensions donats uns punts –que en el nostre cas seran els centres de les cèl·lules. Una part del pla serà d’una regió o d’una altra –en el nostre cas d’una cèl·lula o d’una altra– en funció de quin punt –o centre de la cèl·lula– tingui més a prop.

4. Diagrama de Voronoi per uns quants punts.

Això no obstant, aquesta tècnica només ens descriu una superfície, i per tant no ens serveix per generar el model en tres dimensions de les cèl·lules. La part clau de l’estudi va ser generalitzar aquesta tècnica a les tres dimensions, fent projeccions dels centres a les diferents superfícies i aplicant el mètode de Voronoi diverses vegades.

Una nova forma apareix

Fent això, els científics van descobrir que el model prediu cèl·lules que no tenien forma de prisma ni de tronc, sinó d’una mena de prisma estrany que tenia com a base un pentàgon i com a tapa un hexàgon. Per unir aquestes dues tapes, una de les arestes laterals estava partida formant una forma de Y. Van anomenar aquesta nova figura escutoid.

5. Escutoid

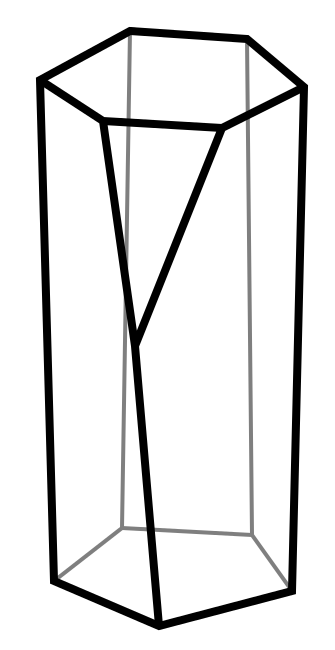
Aquesta figura, evidentment, sempre ha existit, però mai ningú havia tingut necessitat de descriure-la i donar-li un nom. Ara, resol un problema biològic, ja que en empaquetar quatre cèl·lules, les tapes i les bases intercanvien veïns.

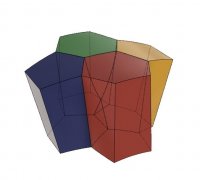
6. Quatre escutoids –que modelitzen cèl·lules del teixit epitelial–  junts intercanvien veïns entre la superfície de dalt i la de baix. En aquest cas, veiem que a dalt els escutoids verd i vermell estan en contacte mentre que a la superfície de baix ho estan el groc i el blau.

I van trobar la nova figura a la natura!

Tot això està molt bé sobre el paper, però és només un model. Perquè sigui un model bo, ha de descriure la realitat, és a dir, hem de veure si realment les cèl·lules l’empaqueten d’aquesta forma en organismes vius. 

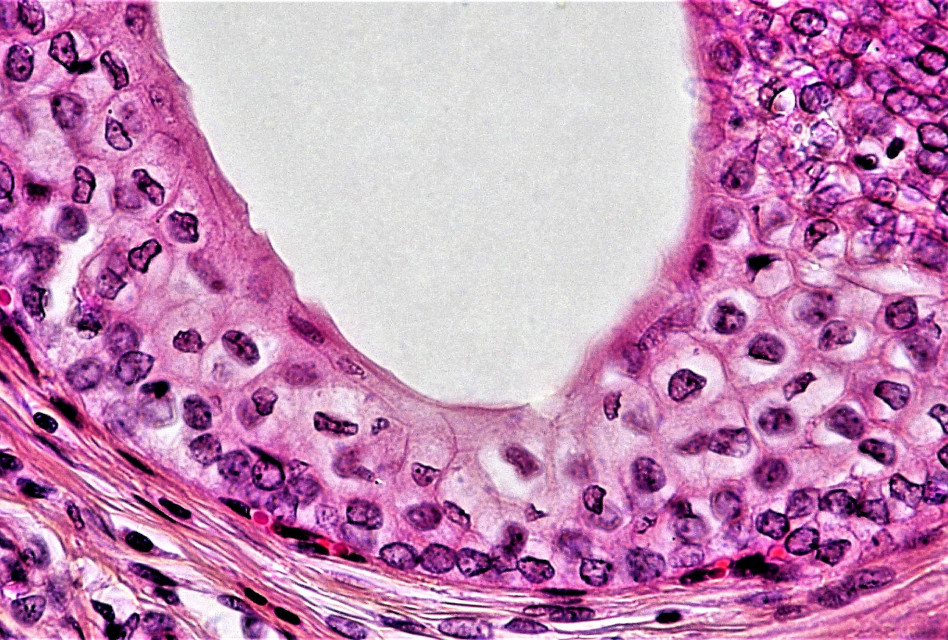
Els investigadors van estudiar una glàndula salival d’una mosca de la mel –que creix en forma cilíndrica– i van veure que les cèl·lules s’organitzaven en forma d’escutoids. És a dir, el nou model és una gran millora respecte a l’anterior!

Finalment, per intentar respondre per què es forma aquesta figura, els físics del projecte van poder determinar que els escutoids minimitzen l’energia necessària per formar teixits en superfícies corbades. És a dir, les cèl·lules hauran de gastar més energia per recobrir una superfície corbada amb qualsevol altra figura geomètrica.  És per això que trobem aquestes figures a la natura!

Ja per acabar

Aquest impressionant descobriment és un exemple de l’increïble treball multidisciplinari entre diferents branques de coneixement. Enfocar un problema des de diferents angles serveix per fer avançar el coneixement i la ciència i, a vegades, descobrir una nova figura!

Per cert!

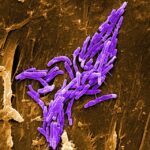
El nom ve per la similitud amb la part d’alguns escarabats, que s’anomena scutum:

7. La part central de l’escarabat es diu scutum, d’on prové el nom escutoid per la seva semblança.

Per saber-ne més

Nature Communications – Scutoids are a geometrical solution to three-dimensional packing of epithelia

El País – Hemos descrito un nuevo objeto geométrico y lo llevas puesto

Stand-up Maths – THE SCUTOID: did scientists discover a new shape?

Fotografies: 2, 3 i 7 extreta de l’article original: Goméz-Gálvez et al. Nat. Commun. 9 (2018); 4 de Balu Ertl; 5 de la Viquipèdia i 6 de JohnPep.