Si tenim dos cistells amb un nombre finit de fruites, ens és molt fàcil comparar-los i saber a quin n’hi ha més i a quin n’hi ha menys però, com ho podem fer si en tenen un nombre infinit? A finals del segle XIX, el matemàtic alemany Georg Cantor ens va descobrir els secrets de l’infinit i des de llavors aquest tema ha fascinat a tothom qui l’ha tractat. Com deia David Hilbert (un altre gran matemàtic), “Ningú no ens podrà expulsar del paradís que Cantor ha creat per a nosaltres”.
Comptem!
Portem comptant des de la prehistòria. Ens ha servit per saber quants animals teníem, per saber si una botiga perd diners o si algú ens ha robat una poma. Així, comptar els elements d’un conjunt d’objectes és prou fàcil. Si tenim un bol amb pomes, només cal que donem un número a cada una fins que s’acabin i sabrem quantes n’hi ha.
Però, com podem comptar els elements d’un conjunt infinit?
Fàcil: ho fem com abans. Comencem per l’u, després el dos i així anem avançant. Però costarà molt i ens durà força temps. De fet, ens morirem abans d’arribar-hi (i això si no ens descomptem!). Potser arribem fins a mil milions, però així i tot ens moriríem sense poder arribar a dir mil milions u. Podríem organitzar una cadena de relleus humana i anar-nos succeint a l’hora de comptar. Però tindríem un problema, i és que, segons els físics, per culpa de l’expansió de l’univers, el temps mateix s’acabarà i no hauríem aconseguit arribar a l’infinit: encara tindríem números més grans per assolir.
De fet, podeu pensar en el número més gran que se us acudeixi i sempre n’hi haurà de més grans. Aquesta és, de fet, la gràcia de l’infinit (o el seu problema!). Aquesta estratègia no ens serà útil. N’haurem de pensar una altra.
Com podem doncs comparar dos conjunts infinits? Una bona idea és fer parelles. Si, com abans, tenim dos cistells, un amb peres i l’altre amb pomes, anem ajuntant una fruita de cada cistell fins que s’acaben a un dels dos. Quan això passi, sabrem que al cistell on s’han acabat primer hi havia menys elements que a l’altre i, si s’acaben al mateix temps, que n’hi havia la mateixa quantitat.
Un hotel molt gran
Permeteu-me viatjar fins a un hotel bastant particular, ja que té infinites habitacions. Cadascuna té el seu corresponent número: l’1, el 2, i així fins a l’infinit. És bo treballar en un hotel infinit si està tot ple (ja que guanyes infinits diners) però un drama si queda buit (ja que té infinites pèrdues). En fi, ens hem d’assegurar de poder omplir totes les habitacions. Usarem les habitacions de l’hotel per fer les parelles que dèiem abans.
Aquesta bonica metàfora va ser proposada per Hilbert i, com és evident, li correspon a en Cantor ser-ne el conserge. En aquest cas, els elements del nostre conjunt no seran pomes sinó persones que es volen allotjar al nostre fantàstic hotel.
Arriben els primers hostes
Arriba un autobús d’aquells de viatges organitzats per allotjar-se a l’hotel. Però, com tot en aquest article, és un autobús infinit. Igualment, és fàcil numerar cada seient i així assignar a cada passatger una habitació. Tenim doncs l’hotel ple. Quan ja tothom s’ha instal·lat a la seva habitació, arriba un turista despistat que també s’hi vol allotjar. Un recepcionista qualsevol li diria que l’hotel està ple, però en Cantor no s’atabala i li diu que en un moment fa lloc per a ell. Demana a tots els hostes que es desplacin una habitació a la dreta. El que estava a l’habitació 1 passa a la 2, el de la 2 passa a la 3 i així successivament. Ho podem fer perquè l’hotel té infinites habitacions i després d’una sempre n’hi ha una més. Així hem alliberat la primera habitació per a aquest turista que ha arribat tard.
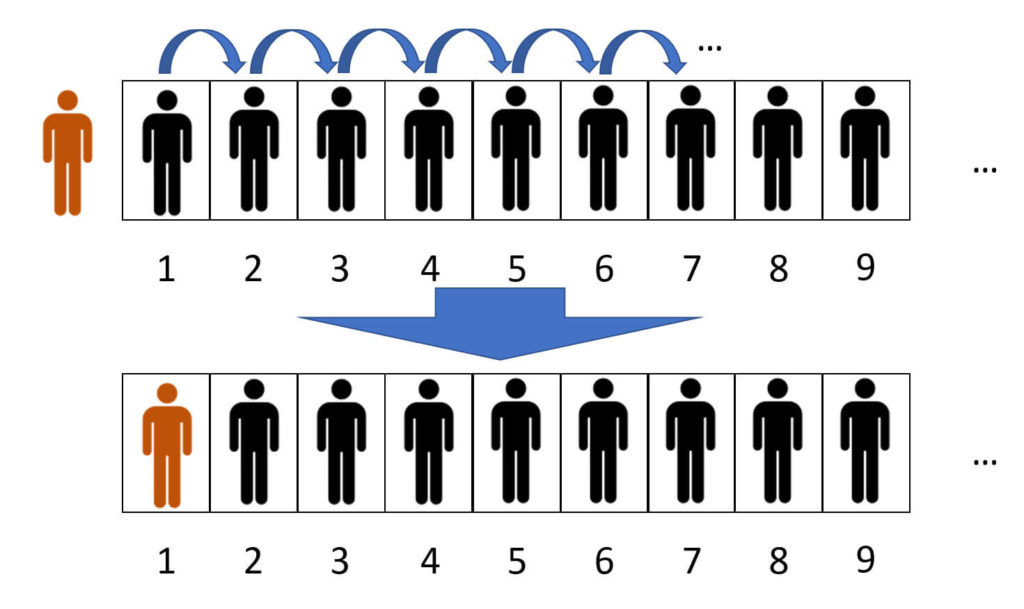
És a dir, els dos conjunts (el del bus sol i el del bus més el turista despistat) ens caben a l’hotel. Així, per la tècnica de les parelles veiem que els dos conjunts s’acaben al mateix temps quan els anem emparellant. Tenen el mateix nombre d’elements! La intuïció ens ha fallat, semblava que hi hauria un element més, però hem vist que n’hi ha el mateix nombre.
Arriba a l’hotel un altre bus infinit
Ara veurem un resultat encara més sorprenent. Suposem que arriba un altre autobús infinit a l’hotel (amb cada seient ben numerat com abans). No podem fer servir la mateixa tàctica, ja que no podem demanar als actuals hostes que es moguin infinites habitacions a la dreta; no sabem què és infinit (és, de fet, el nostre gran problema). Els haurem de dir que es moguin a una posició concreta.
Podria semblar que ja està, que aquest infinit no ens cap a l’hotel, que hem trobat un infinit més gran que el que teníem inicialment. Però el nostre conserge no tira la tovallola. En Cantor ens recorda que a la nostra llista d’habitacions n’hi trobem infinites amb un nombre parell i infinites amb un nombre senar. Així que envia cada persona ja allotjada a l’habitació amb el doble del número que té; si estava a la 1, l’envia a la 2, el de la 2 a la 4, … el de l’habitació n a la 2n (ho podem fer perquè estem enviant cada persona a una habitació en concret i com que n’hi ha infinites aquesta sempre existirà). Això allibera totes les habitacions senars: la 1, la 3, la 5… Només cal allotjar cada membre del nou bus a una d’aquestes i ja estaria; per exemple enviant la persona del seient n a l’habitació 2n-1 (el del seient 1 a la 1, el de la 2 a la 3, etc.).
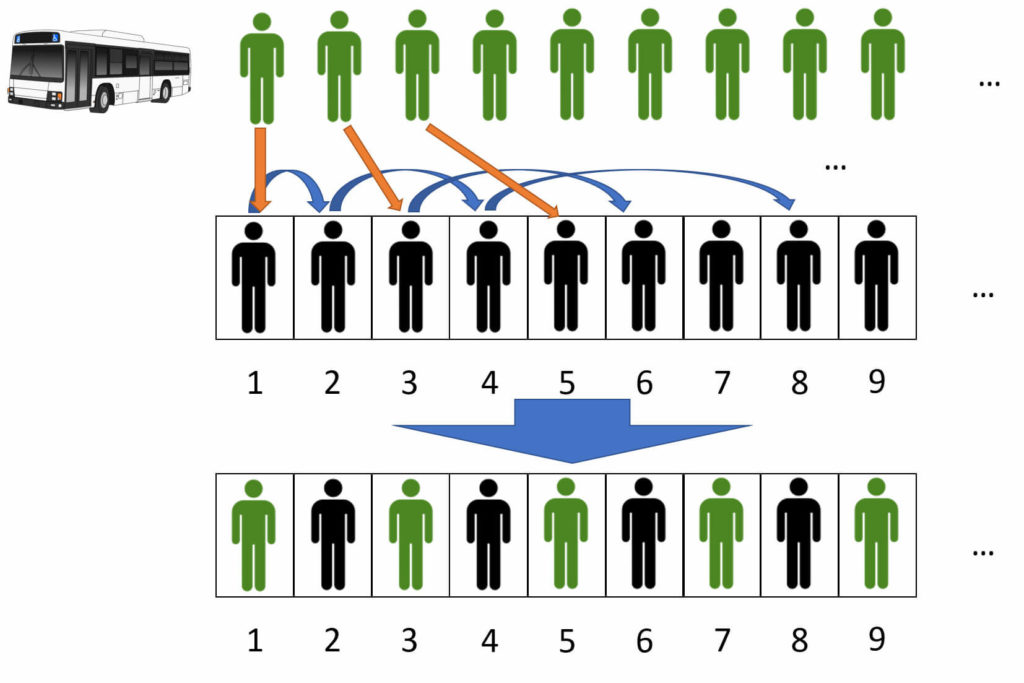
Hem vist una cosa sorprenent! Aparentment semblava que hauríem de tenir el doble de persones, però al final el nou autobús ha cabut a l’hotel i per tant els dos infinits són iguals (el de l’hotel, o d’un bus sol, i el dels dos busos infinits). Com ho hem vist? Hem fet aquella tècnica d’emparellar objectes de dos conjunts; el de les habitacions de l’hotel i el de les persones als dos busos infinits. Cada habitació correspon a una (única!) persona dels dos busos i no ha quedat cap persona per col·locar, així, el nombre d’habitacions és el mateix que el nombre de persones als dos busos.
Ja per acabar…
Arribats a aquest punt ens semblaria que tots els conjunts infinits tenen el mateix nombre d’elements. Però encara queda un últim bus per arribar a l’hotel. Això, tanmateix, ja és una altra història…
Per saber-ne més
European Mathematical Society – How to Count to Infinity
Derivando – ¿Existen infinitos más grandes que otros?
Numberphile – Infinity is bigger than you think








