Imagina que fa temps que mires diferents models de mòbils i finalment et decideixes a comprar-ne un que val 800 €. Vas fins a la botiga (perquè això de comprar per internet, a tu, no et va), demanes el que vols i et presentes al taulell amb la targeta de dèbit a la mà. En aquest moment, la persona que t’atén et fa la maleïda pregunta: “Vols incloure-hi una assegurança a tot risc per només 150 €?”. I ara, què fas? Agafar l’assegurança, no fos cas que el mòbil caigués dins la tassa del vàter i se n’anés tot en orris? O no agafar-la perquè, al cap i a la fi, mai has tingut cap desgràcia monstruosa amb els anteriors mòbils?

Creus que és una bona idea contractar una assegurança? En aquest reportatge veurem què en diuen les matemàtiques per posar punt final a aquest dilema!

La llei dels grans nombres

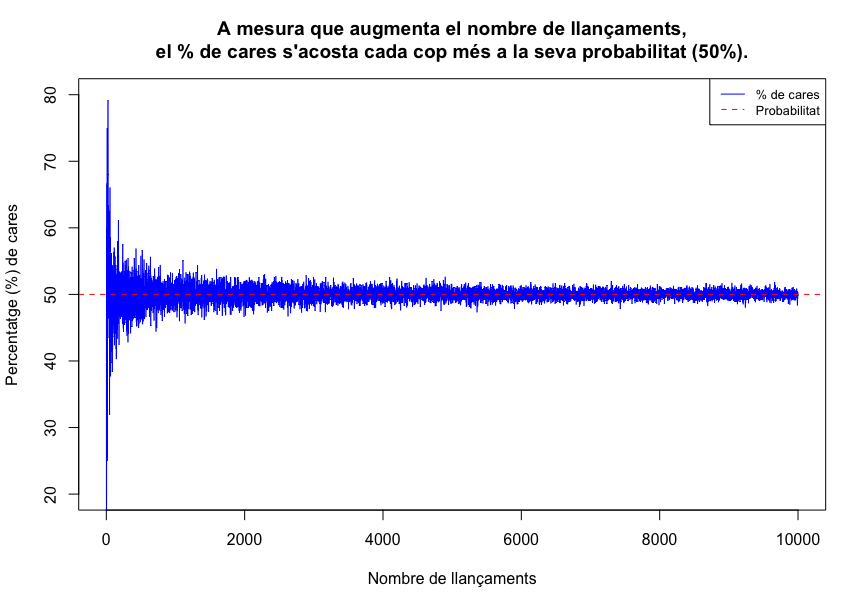
Comencem parlant de la mare dels ous: la llei dels grans nombres. D’acord amb aquest principi, en un conjunt de dades prou gran, la freqüència d’un esdeveniment tendeix a apropar-se a la seva probabilitat real. Posem un exemple per veure-ho millor. Si llancem una moneda, aquesta té un 50% de probabilitats que surti cara, i un altre 50% que surti creu. Suposem que llancem la moneda 10 vegades i obtenim 6 cares i 4 creus, la qual cosa no és exactament el 50%. Tanmateix, com més llançaments fem, més ens acostarem al percentatge del 50%, és a dir, més a prop estarem de la seva probabilitat teòrica.

La matemàtica de les assegurances

Ens movem ara cap al moll de l’os i desgranem una mica el món de les assegurances per entendre com funcionen. En primer lloc, la quantitat que pago com a client és la prima, i varia en funció del tipus d’assegurança i del valor de l’objecte, però també de l’edat i de les condicions de salut de la persona si es tractés d’una assegurança mèdica. Una mica més endavant veurem com s’ho fan per calcular aquesta prima.

Abans, però, introduïm un nou concepte: la probabilitat de sinistralitat. Aquesta probabilitat es pot aproximar a partir de dades històriques i fent servir diferents models estadístics. Per exemple, per calcular la probabilitat corresponent a haver de canviar el mòbil per un de nou, mirem les dades dels últims anys. Quants accidents es van produir? I exactament com varia aquesta proporció si només mirem a gent de la meva edat? I si ens fixem només en aquesta marca de mòbil? Totes aquestes dades fan que la probabilitat de sinistralitat variï.

L’esperança (de beneficis)

Un cop tenim la probabilitat de sinistralitat, l’asseguradora ha de posar un preu a la prima. Per fer-ho, fa servir un càlcul estadístic anomenat esperança que els permet preveure les possibles pèrdues o guanys associats a aquesta probabilitat. Per calcular l’esperança, només cal sumar el valor dels resultats possibles ponderats per la seva probabilitat.

Esperança = Valor 1 x Probabilitat 1 + Valor 2 x Probabilitat 2 + …

En el cas concret de l’assegurança d’un mòbil, suposem que la probabilitat de sinistralitat és del 15% i, com dèiem al principi del reportatge, hem pagat 800 € pel mòbil i una assegurança a tot risc de 150 €. Per tant, l’esperança vindrà associada a aquestes dues situacions:

  • Amb un 85% de probabilitat (100% menys 15%), mai li passa res al mòbil. Com a resultat, l’asseguradora s’estalvia de pagar i s’embutxaca els 150 € de l’assegurança.
  • Amb un 15% de probabilitat, cau el mòbil dins del vàter i, per tant, l’asseguradora m’ha de pagar 800 €. En total, haurà perdut 800 € menys els 150 € que ja vam posar-hi al principi, és a dir, 650 €.

Esperança = 150€ x 0,85 – 650€ x 0,15 = 30€

En conseqüència, l’esperança de la companyia és de guanyar, de mitjana, 30 € de cada persona que contracti una assegurança! Però com és possible si només hi ha dues situacions (perdre 650 € o guanyar 150 €)? El que passa és que estem aplicant la llei dels grans nombres. Com que la població que haurà contractat l’assegurança és bastant gran, la freqüència tendeix a la probabilitat, és a dir, al 15% d’accidents. Per tant, si fem la mitjana dels diners que perdran i guanyaran amb cada persona, ens surt que seria com si guanyessin 30 € de cadascú. L’asseguradora sempre guanya i els clients, en global, hi perdem calés.

Llavors, quan és útil una assegurança?

Jugant a la llei dels grans nombres, una assegurança mai surt rendible a llarg termini. El que passa és que pot ser una eina útil per tothom qui no tingui un bon fons d’estalvi. M’explico: si faig una assegurança a tot risc per al meu mòbil, i en algun moment tinc un accident, l’assegurança farà que no hagi de pagar de cop aquest imprevist. Ara bé, si tinc alguns diners estalviats i sé que aquest imprevist no posarà en risc la meva estabilitat econòmica, el millor és no fer cap assegurança.

El corol·lari vindria a ser el següent: contracta una assegurança només per allò que realment suposaria un daltabaix en la teva economia domèstica.

Ja per acabar…

D’afegitó, podem calcular l’esperança de jugar a la Grossa de Nadal. Simplificant-ho molt, un dècim costa 20 € i la probabilitat que et toquin els 400.000 € és del 0,00001%, així que l’esperança surt de 0,04 €, és a dir, que hi perds més o menys el 95% del diners que et gastes.

Així doncs, la loteria es presenta com una opció poc favorable des del punt de vista probabilistic. Aquesta percepció queda reflectida en la crítica del matemàtic Roger Jones, qui l’anomenava “l’impost per les persones que els van malament les matemàtiques”. No obstant això, a través d’una bona educació financera i matemàtica accessible a tothom, la societat pot estar més ben informada i prendre decisions més conscients envers el joc i els diners.

Per saber-ne més

Charles Wheelan – Naked Statistics: Stripping the Dread from the Data

Educació Digital – Resum dels conceptes bàsics de Probabilitat

Sangaku Maths – Esperança matemàtica

Imatge de portada: TaxRebate