Fer prediccions no és gens fàcil. Per començar, els models que descriuen la meteorologia formen un sistema caòtic. És a dir, que petites variacions en les condicions inicials produeixen resultats molt diferents. A més a més, ens trobem amb un altre problema: les imprecisions en les mesures.
Cap aparell de mesura és perfecte. Tots porten incorporat un petit error que modifica lleugerament el valor real. Pensem, per exemple, en un termòmetre dels d’abans, dels de mercuri. Si la ratlleta del mercuri està exactament entre dues línies, aleshores quin és el valor que marca el termòmetre, el de sobre o el de sota?

Encara més errors!
A part d’aquests errors instrumentals, al món també hi ha aleatorietat, fluctuacions i variacions. Les coses no estan fixes i immòbils: potser fem una mesura i al cap d’un segon el que hem mesurat ja ha variat una mica. Això genera un altre error encara més difícil de controlar, que s’anomena error estadístic.
La predicció del temps de demà dependrà de la pressió atmosfèrica d’avui, i un petit error ens pot fer canviar el pronòstic completament. Així, habitualment ens podem trobar que plou quan estàvem convençuts que faria sol ーarruïnant-nos així aquell acte de la Festa Major del qual teníem tantes ganes.
Com podem ajustar les nostres prediccions, per exemple, del temps que farà demà, tenint en compte aquests errors en les nostres mesures?
Procés estocàstic
Per reduir aquests errors podem fer millors aparells de mesura ーi reduirem l’error instrumentalー i moltes mesures ーper tal de reduir l’error estadístic. Això no obstant, volem anar més enllà i tractar l’error d’una forma contínua. Si estem fent prediccions del temps que farà, les anirem fent cada moment del dia: d’aquesta manera, volem ajustar el nostre model matemàtic que descriu la meteorologia amb les dades que tenim i anar corregint l’error a mesura que van passant les hores.
La part de les matemàtiques on s’estudia el control d’aquests errors és l’estadística i la teoria de probabilitat. Es fa des d’una branca molt concreta que anomenem processos estocàstics: un procés descrit per una probabilitat ーcom la que un dau tregui un nombre concretー però que varia en el temps.
Filtre de Kalman
Una possible tècnica per resoldre aquest problema és l’anomenat filtre de Kalman. Rep el nom del matemàtic hongarès-americà Rudolf Emil Kálmán, que va ser un dels primers impulsors de la teoria. La principal idea del mètode és fer una sèrie de mesures durant un període de temps per produir una estimació d’una variable desconeguda amb més precisió que fent una única mesura.
El cas del cotxe
Posem un exemple senzill per intentar explicar com funciona un d’aquests mètodes per reduir els errors en la mesura.
Estem anant per la carretera amb el navegador del cotxe i entrem en un túnel. El GPS que porta el navegador és prou precís per dir-nos la posició bastant exacta del cotxe, però un cop entrem en el túnel es perd part de la connexió amb el satèl·lit i l’error instrumental de la mesura augmenta moltíssim. Això no obstant, ens hi fixem i sembla que el punt del mapa avanci exactament com ho fem nosaltres. Com pot ser això?
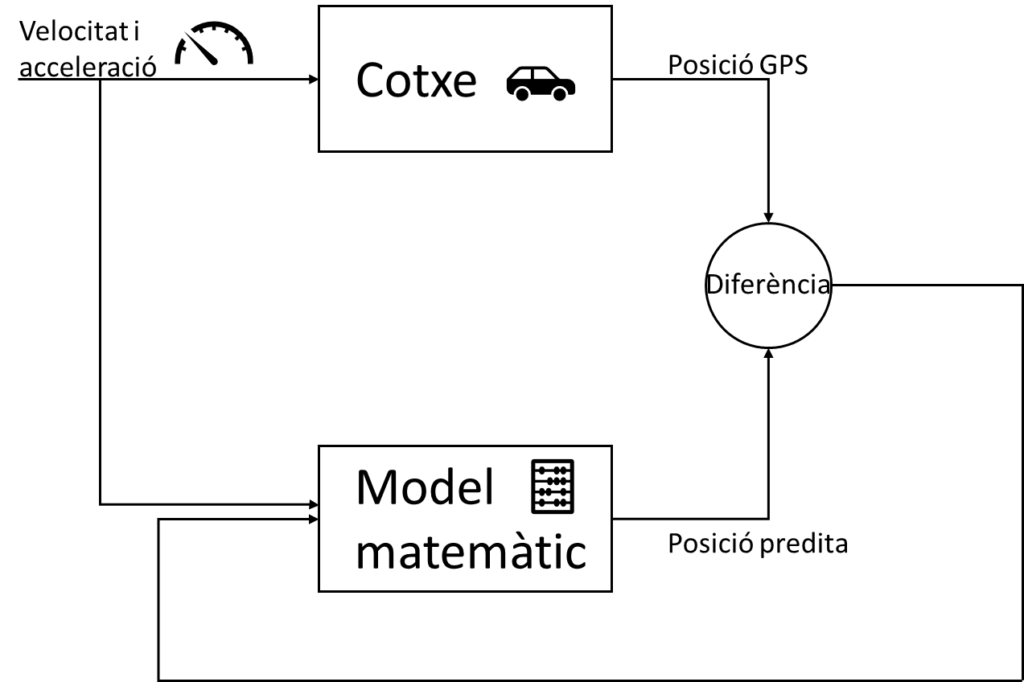
La forma amb la qual el mapa del cotxe resol aquest problema és combinant dues fonts d’informació. Primer de tot, té les dades que li arriben a través del GPS, però que tenen molt d’error. A part, el cotxe està equipat amb tot de sensors, com acceleròmetres i velocímetres que mesuren com varien, respectivament, la seva acceleració i velocitat. En saber aquestes dades, podem derivar un model matemàtic per calcular la posició del cotxe en cada moment. Però aquests aparells també tenen un error prou important i, a part, el model segurament no té en compte dades rellevants com el terreny sobre el qual conduïm, etc.
El que fa el cotxe és ajuntar aquestes dues dades d’una forma intel·ligent. Aplica el model matemàtic per predir la posició de forma contínua i utilitza les dades del GPS per controlar com és de bona aquesta predicció. Així, usa les dades de l’error en la predicció per afinar el model matemàtic i donar una predicció més precisa.
Com s’aplica?
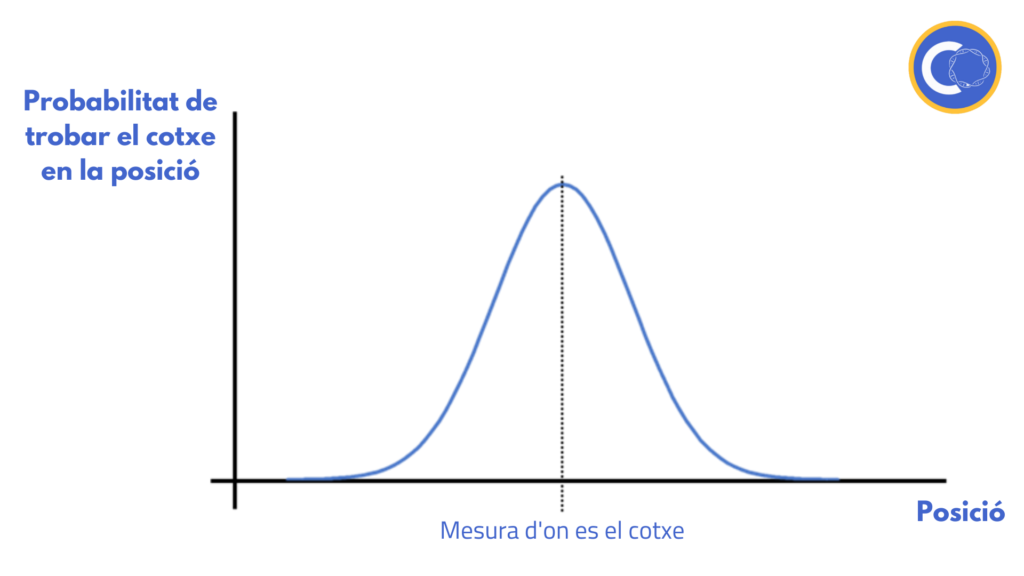
És molt fàcil entendre com funciona el filtre de Kalman d’una forma visual. Suposem que tenim la posició que ens dona el GPS i la del model matemàtic com a un punt. Això no obstant, hi ha el maleït error del qual parlem tota l’estona. Així, podem descriure la posició del cotxe com una probabilitat:
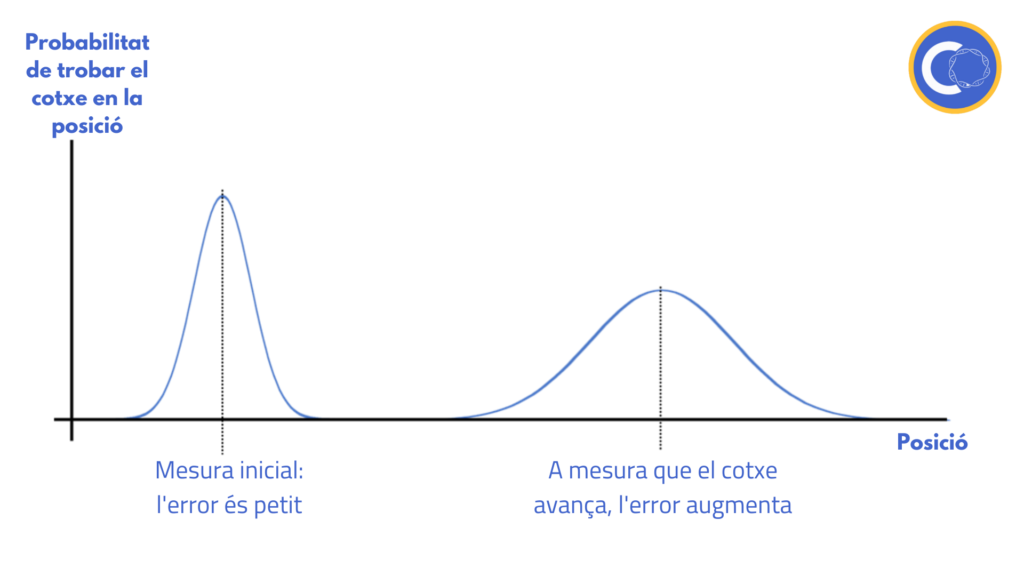
Al principi, el cotxe té un error petit en l’estimació mitjançant el model matemàtic, però a mesura que anem avançant, l’error es va incrementant ーja que com hem dit, no tenim en compte el terreny o el nostre velocímetre no és prou precís.
A part, la mesura del GPS també té un error inclòs:
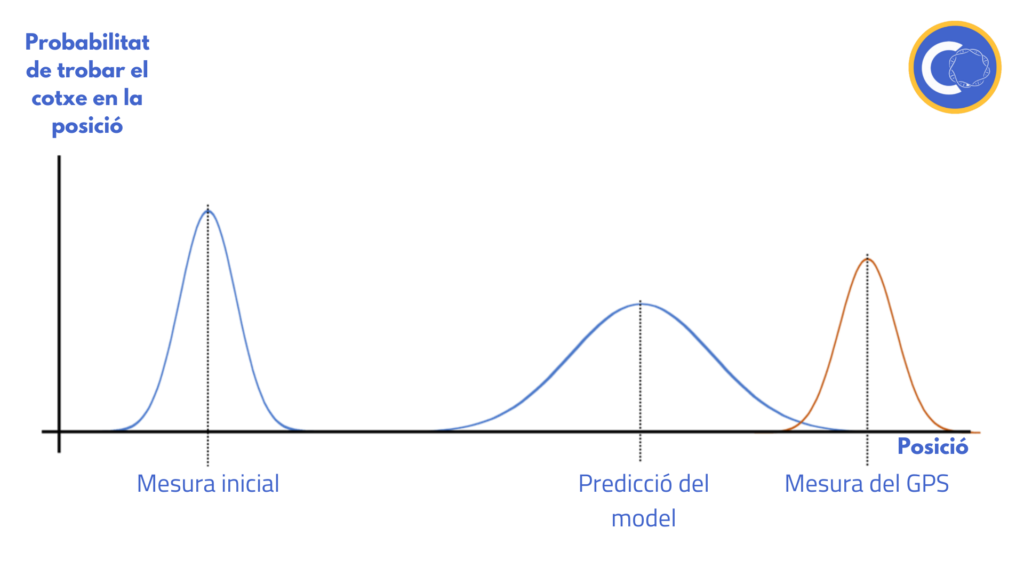
Grosso modo, el filtre de Kalman multiplica aquestes dues probabilitats de forma que n’obté una nova de la posició del cotxe que és molt més acurada que les dues anteriors:
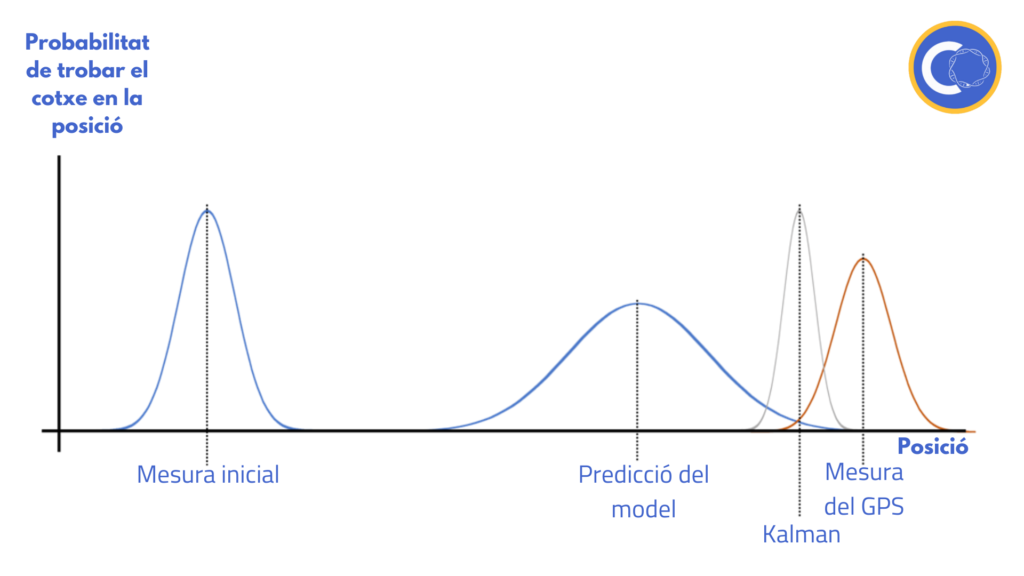
Aquesta nova posició calculada és la que el mapa del navegador ens mostrarà a la pantalla i així ens semblarà que no hi ha quasi cap error.
Ja per acabar…
Aquesta tècnica s’utilitza per predir el temps a llarg termini. El Centre Europeu per Prediccions de Termini Mitjà o ECMWF per les seves sigles en anglès (European Centre for Medium-Range Weather Forecasts) utiliza el filtre de Kalman per millorar les seves prediccions. Així, no només fa servir models físics per predir com serà el clima els propers mesos sinó que a més utilitza les dades reals i l’estadística per modificar i ajustar constantment el model.
Amb el filtre de Kalman s’obtenen prediccions més acurades!
Per saber-ne més
ECMWF – About our forecasts
Viquipèdia – Filtre de Kalman
Bzarg – How a Kalman filter works, in pictures
Els esquemes són d’elaboració pròpia a partir d’un exemple de MATLAB. Vull agrair a Flàvia Ferrús l’ajuda en aquest article.