A Ciència Oberta ens han anat molt bé aquestes vacances de Nadal. Això no obstant, han aparegut tot de qüestions matemàtiques importants que en algun moment haurem d’adreçar. Avui, a dia 8 de gener, em proposo tractar-ne algunes i així començar el nou any amb uns quants problemes menys!

1r problema: Guardant els canelons

La meva família sempre fa canelons de més, i és clar, llavors surt el drama d’haver-los de guardar. En general, els congelem. Per fer-ho, cal posar-los en una carmanyola, però la seva forma cilíndrica no ens ho posa fàcil. Si volem omplir la carmanyola del tot, fent diverses files de canelons, no podrem, ja que quedaran buits produïts per la forma circular del lateral del caneló.

1. Si fem servir canelons cilíndrics quedarà espai buit. (Sí, a casa som molt especials i congelem els canelons apilats, què passa?!)

Aquesta és una pregunta típica de matemàtiques. Tradicionalment, s’ha plantejat com enrajolar un terra de forma que no quedin buits –tot i que a mi m’agrada més la versió nadalenca amb canelons! Sabem que amb rajoles quadrades o hexagonals és fàcil. La pregunta és: amb quines formes serem capaços de fer-ho? També ens podem preguntar què passa si considerem rajoles de formes diferents. Fins i tot podríem pensar si podem generalitzar l’enrajolament a més dimensions…

Aquestes preguntes tenen respostes que variaran en cada cas considerat i que, en molts casos, són un problema obert en les matemàtiques. En el primer “Per saber-ne més” us deixo un bon article de resum sobre l’enrajolament no periòdic, aquell on les rajoles no formen patrons.

2n problema: Avui és el meu aniversari

Durant el sopar de l’últim dia de l’any, una amiga em comenta que deu fer molta mandra celebrar l’aniversari al dia 1 de gener, ja que se t’ajunta tot. La qüestió és que això em va fer pensar que la meva amiga Queralt fa anys aquell dia. La Queralt va menjar el raïm a Maria Cristina, veient l’espectacle de drons amb unes 1500 persones més –bé, allà hi havia 120 mil persones, però comptem només les que estaven més a prop seu. Una pregunta que ens podem fer és quina és la probabilitat que entre aquestes 1500 persones, n’hi hagi una altra que faci anys el mateix 1 de gener –i així, felicitar-se i compartir les penes. Però aquesta pregunta no m’interessa i com a bon matemàtic la deixo d’exercici al lector. 

M’interessa molt més el que pensa la Laura, amiga de la Queralt, que és molt supersticiosa. Ella diu que quan menges el raïm d’any nou amb una persona que fa l’aniversari el mateix dia que tu, aquell any acabareu casant-vos; per un tema de l’horòscop o algo així –sé que qualsevol astròleg de tres al quarto ens diria que l’horòscop no funciona així, però això és el que pensa la Laura i aquí no som ningú per qüestionar les creences irracionals de la gent.

En qualsevol cas, podem pensar que, més o menys, les 1500 persones que hi havia veient els drons van menjar el raïm juntes. Hi haurà casaments? Sí! Perquè per força més de dues persones hauran nascut al mateix dia de l’any.

2. Com a mínim 2 coloms hauran de compartir gàbia.

Això és pel principi del colomar: si tens 10 gàbies i 11 coloms, no podràs posar cada colom sol a una gàbia. Com a mínim en una de les gàbies hi hauràs de posar 2 coloms. En el nostre cas, tenim 366 dies i 1500 persones, per tant, com a mínim hi haurà 4 persones que celebraran l’aniversari el mateix dia menjant el raïm juntes –tot i que no sé com va el tema legal d’una tetraboda.

3r problema: Salutacions per Cap d’Any

Cadascú celebra la nit de Cap d’Any com li ve de gust i jo em vaig trobar ballant en una discoteca amb més de 300 persones. Casualment, el nostre estimat corrector, en Víctor, també estava allà passant l’estona. En Víctor, que és molt considerat, desitjava bon any a tothom amb qui es creuava i els saludava donant la mà. En canvi, jo, que tinc molt mala llet, m’enfadava amb els coneguts que, en passar pel meu costat, no em saludaven –i evidentment tampoc els saludava jo, què s’han pensat!

Per estar tots contents, cadascuna de les persones que estava per allà pul·lulant, s’hauria d’haver saludat amb tota la resta de gent. Ens trobem davant del típic problema de les encaixades de mans. Quantes encaixades de mans s’haurien fet si tothom s’hagués saludat?

La versió naïf d’atacar el problema és: cada persona saluda a tota la resta, és a dir, cada persona fa 299 salutacions –no ens saludem a nosaltres mateixos, habitualment. Per tant, el nombre d’encaixades és 300 vegades 299 encaixades. Però això clarament no és cert, ja que estaríem comptant cada encaixada dos cops. Estem comptant que jo vaig saludar a en Víctor i estem contant de nou que ell em va saludar a mi, quan en realitat ens vam saludar un cop i ja –tampoc cal passar-se de simpàtics.

Abordem el problema amb una mica més de gràcia… La primera persona que es posi a saludar, haurà de saludar a tothom, és a dir, a 299 persones. La segona, en canvi, ja s’haurà saludat amb la primera i, per tant, només haurà de fer 298 encaixades de mans. La tercera –que ja estarà farta de la primera i la segona– només n’haurà de fer 297. Així fins a l’última persona, que no haurà de saludar a ningú.

És a dir, hem de calcular la suma 

    \[299 + 298 + 297 + \cdots + 1\]

aquesta suma és molt interessant i correspon a una sèrie matemàtica que es diu els nombres triangulars. En aquest cas, hem de calcular el nombre triangular 299. 

Mirem-nos-ho amb només 4 persones per trobar una bona fórmula. En aquest cas hem de calcular 4+3+2+1. Per escriure aquesta sèrie en forma de triangle –per això es diuen nombres triangulars– farem files de tants punts com cada terme de la suma:

3. Escrivim la suma com un triangle de punts

Així, per fer la suma només cal comptar quants punts hi ha, però podem fer un truc, copiar el triangle a dalt per obtenir un quadrat i comptar els punts del quadrat multiplicant el nombre de punts de la base pels de l’alçada.

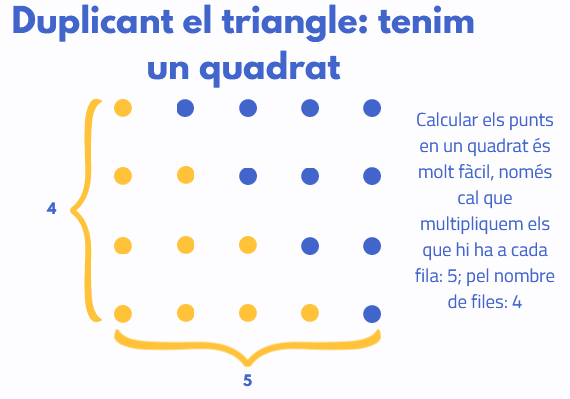
4. Si dupliquem el triangle obtenim un quadrat, on comptar els punts és molt fàcil

Així, si considerem que els punts originals són la meitat dels que tenim al quadrat,

    \[4+3+2+1 = \frac{5 \cdot 4}{2}\]

Podem repetir el raonament per qualsevol nombre triangular i obtindrem una fórmula general! Ja podem comptar ràpidament quantes encaixades s’haurien d’haver fet la nit de Cap d’Any:

    \[\frac{300 \cdot 299}{2} = 44859\]

S’haurien d’haver fet 44859 encaixades! Potser millor dedicar-se a ballar…

Aquest problema que sembla naïf, ens porta a parlar de teoria de nombres, un camp de les matemàtiques que encara continua avançant i produint resultats sorprenents. Potser és moment de fer balanç i mirar en vista d’ocell com han canviat les matemàtiques aquest darrer any. Evidentment, no ho farem aquí, però si a algú li interessa pot mirar aquest article de divulgació que en parla.

4t problema: Els reis són màgics

Evidentment encara queda parlar dels Reis! I hi ha moltes preguntes matemàtiques per resoldre: com s’ho fan per ser a tot arreu en una sola nit? A quina velocitat han de viatjar? Per quantes cases han de passar? Quina és la probabilitat que es deixin el meu regal?

Però m’he quedat sense espai i deixaré que algú altre les respongui! Per exemple, en Toni de Del Buit al Tot que ens parla de l’estel de Nadal.

Molt bon any a tothom i que estigui ple de matemàtiques!

Per saber-ne més

Quanta Magazin – ‘Nasty’ Geometry Breaks Decades-Old Tiling Conjecture

Viquipèdia – Principi de les caselles

singingbanana – The Maths of Christmas

Els esquemes són d’elaboració pròpia.