Es diu que el nombre auri és un nombre harmoniós, bonic, que ens dona tranquil·litat i que la majoria d’obres magnes de l’ésser humà estan basades en aquest nombre. Però, què té de cert això? És un número com qualsevol altre o té alguna propietat que el fa especial?

    \[\Phi = \frac{1+\sqrt{5}}{2} \approx 1,61803\]

Com ja vam parlar fa temps a Ciència Oberta, el nombre o la proporció àuria ens produeix assossec als humans perquè és un nombre que trobem a tot arreu a la natura. La pregunta que ens hem de fer ara és evident: què li passa a aquest nombre perquè hi sigui tan present?

Criar com conills

Abans de parlar de què el fa tan especial, permeteu-me anar a veure un exemple més de llocs inesperats on apareix. Volem estudiar com evoluciona el naixement de conills al llarg del temps. Un problema al qual es va adreçar el matemàtic italià Leonardo de Pisa, més conegut com a Leonardo Fibonacci.

Al fer aquest tipus d’estudis no ens interessa fer una descripció exacta del nombre d’individus, sinó només veure la tendència general. Això ens és molt útil, ja que ens permet entendre certs comportaments, com ara perquè els lèmmings desapareixen cada quatre anys. D’aquesta manera, podem fer suposicions fortes —i irreals— respecte com crien els conills i el nombre inicial que tenim.

Comptem els conills per parelles, formades per una femella i un mascle. Suposem que al principi només tenim una parella. Imaginem que es reprodueixen un cop al primer mes i un altre al segon mes de vida, i que, cada vegada que ho fan, la descendència és un mascle i una femella que també s’ajuntaran—això és irreal però ens permet fer-nos una idea de com evolucionen.

D’aquesta forma al primer mes hi haurà una sola parella de nounats —els fills de la parella inicial—, el segon mes dues parelles de nounats —els segons fills de la inicial i els fills de la primera parella. El tercer hi haurà 3 parelles de nounats, els fills de la parella del 1r mes i els fills de les dues parelles del 2n mes. 

1. Esquema del nostre model de reproducció dels conills

Si posem Rₙ a les parelles que neixen al mes n, tenim el següent diagrama:

El nombre de parelles nascudes a cada mes és la suma del nombre de parelles nascudes als dos mesos anteriors. Obtenim la seqüència següent:

1, 1, 2, 3, 5, 8, 13, 21…

Molt coneguda: és la successió de Fibonacci! Però, quina relació té el nombre d’or amb aquesta successió? Estan molt relacionats: si dividim un element entre l’anterior, trobarem una aproximació cada cop millor del nombre auri. A més, podem escriure qualsevol element de la successió com:

    \[R_n =\frac{1}{\sqrt{5}}\left[ \Phi^n - \left( \frac{-1}{\Phi} \right)^n \right]\]

On 𝚽 és la raó àuria, és a dir,  𝚽 = 1,61803. Si useu la fórmula anterior per unes quantes n  —el mes en el qual volem calcular els nounats— veureu com aneu obtenint els elements de la famosa successió. És a dir, la raó àuria està íntimament relacionada amb la successió de Fibonacci! D’aquesta manera podem calcular que en només un any, tindrem 144 noves parelles. En dos anys ja en tindrem 46368 i en tres 14930352!!! Només ens cal canviar la n per 12, 24 o 36 mesos.

El constructor de flors

El següent problema al qual ens enfrontem és com construir un bon fruit o una bona flor. Volem construir el fruit anant posant llavors al voltant d’un centre. És a dir, imaginem que som una planta, i que la nostra estratègia per fer-ho és col·locar una llavor, girar una certa quantitat fixa, col·locar la llavor següent, tornar a girar, col·locar llavor… Anem a veure com quedaria prenent diferents quantitats de gir.

Girant una volta completa cada vegada És una forma bastant dolenta de fer una flor. Tornem cada vegada al mateix punt i obtenim només una filera de llavors. No ens interessa!
Girant 1/3 de volta cada vegada En aquest cas tenim tres files de llavors. Tampoc és una estratègia massa bona. Observem que si posem que giri 2/6 de volta també obtenim la mateixa figura. Les flors saben simplificar fraccions! Per contra si posem que giri 1/10 de volta, veurem 10 files de llavors. Ens passarà el mateix amb qualsevol racional.
Girant π volta cada vegada Hem vist que amb els nombres racionals no obtenim una flor bonica, ja que al poder-los escriure com a fracció ens apareixen files de flors. Triem un nombre irracional per intentar que això no passi… En aquest cas triem el nombre irracional per excel·lència: π. Però, tot i que al principi no es veuen files, de seguida en podem observar —a pesar de no ser rectes. Continua sense ser una bona flor!

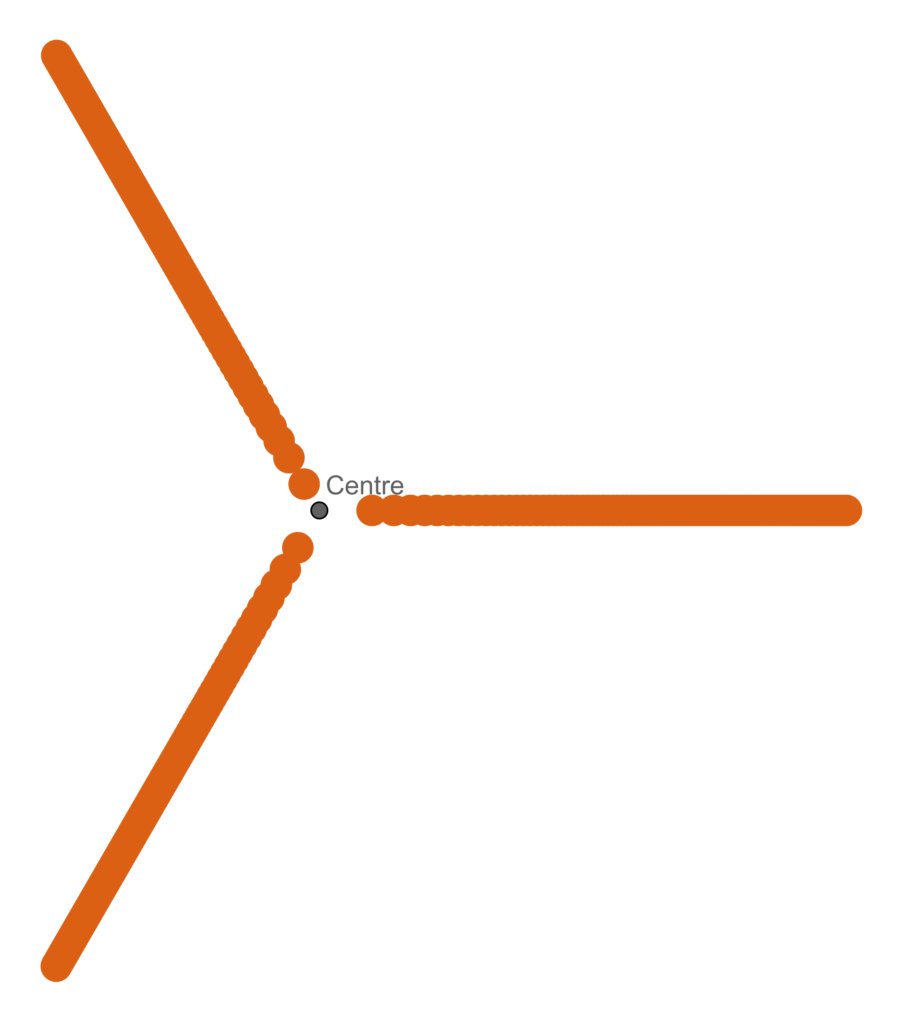
Per què el nombre π no ens fa una bona flor?

Per explicar-ho haurem d’escriure π en forma de fracció contínua. Sabem que 

    \[\pi \approx 3,14159\dots\]

però també el podem escriure com la part entera més una part decimal. És a dir

    \[\pi = 3 + \text{part decimal}\]

aquesta part decimal la podem escriure com 1 dividit entre un número, aquest número serà 7,06251… És a dir,

    \[\pi = 3 + \frac{1}{7,06251\dots}\]

Per aquest nou número podem fer el mateix, separar-lo entre part entera i decimal i així anar encadenant fraccions.  D’aquesta forma obtenim que

    \[\pi = 3 + \cfrac{1}{7+\cfrac{1}{15+\cdots}}\]

Ho podeu comprovar amb la calculadora! Com que el 15 és un nombre bastant gran, la suma amb tot el que vingui a continuació serà petita —perquè l’estem dividint— i per tant aportarà molt poc a la suma total. És a dir, el nombre π s’aproxima molt bé per 

    \[3+\frac{1}{7}= \frac{22}{7}\]

i per això veiem 7 files a la flor. Si anéssim augmentant el nombre de llavors veuríem aparèixer altres aproximacions de pi, però sempre formant aquestes files tan clares que no ens permeten empaquetar bé les llavors!

El nombre de les flors

Per fer una bona flor, volem evitar que ens apareguin aquestes files. És a dir, volem que la fracció contínua no hi hagi cap nombre “gran” com el 15 del π. La millor opció possible serà quan a la fracció contínua hi trobem només uns:

    \[ 1 + \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}}\]

Podríem dir que aquest nombre serà el més irracional, ja que no es podrà aproximar bé per cap fracció. Però hem de trobar-lo per posar-lo al nostre constructor de flors! Comencem dient-li x. Un fet clau és que, si ens hi fixem, dins de la fracció hi ha el mateix nombre x que volem calcular repetit:

    \[x = 1 + \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}}} = 1+ \frac{1}{x}\]

Ara només es tracta de solucionar l’equació. Podríem aplicar la fórmula de les equacions de grau dos, però aquí ho farem completant quadrats —que és, de fet, d’on surt la formula. No en comento els detalls, ja que només ens interessa el resultat:

    \[x = 1 + \frac{1}{x} \Leftrightarrow x^2 = x+1\]

    \[\Leftrightarrow x^2-x-1 = 0 \Leftrightarrow \left(x - \frac{1}{2} \right)^2 - \frac{1}{4} - 1 = 0\]

    \[\Leftrightarrow x - \frac{1}{2} = \pm \frac{\sqrt{5}}{2}\]

    \[x = \frac{1\pm \sqrt{5}}{2} = \Phi\]

Hem trobat que la flor més “bona” serà la construïda quan girem cada vegada el nombre auri de voltes! Fortíssim!

2. Flor feta girant la raó àuria de voltes entre llavor i llavor.

De fet, aquesta és la forma que tenen molts fruits de les plantes. Per exemple les llavors a la inflorescència dels gira-sols, la disposició de les fulles de la carxofa o els pinyons a una pinya.

Podeu jugar amb l’animació del constructor de flors al següent applet. Es pot modificar el nombre de llavors (N), el gir i la velocitat de l’animació. Aquí podeu veure el cas dels racionals que generen files de llavors i altres irracionals famosos.

Ja per acabar…

Hem vist que el nombre d’or, a part de venir d’una relació particular entre dos segments també és el que presenta una de les característiques més particulars d’entre tots els irracionals! Aquí és exactament on rau la bellesa del nombre d’or. Podríem inclús dir que és el nombre més irracional. Les plantes han sabut trobar-lo entre tots els nombres possibles per poder empaquetar de la millor manera possible les seves llavors i és omnipresent a la natura. Segurament, per això el nombre d’or és l’or entre els nombres!

Per saber-ne més

Numberphile – The Golden Ratio (why it is so irrational)

SciFri  – Creating The Never-Ending Bloom

Derivando – La sucesión de Fibonacci y la razón aúrea

Les simulacions són fetes usant GeoGebra.(3) i la portada és d’en Luca Postpischi (Flickr). (5) és de Arbyreed (Flickr).