Sumar és una operació matemàtica aparentment senzilla. És la primera que aprenem i segurament tots recordem. Sumar un nombre finit de quantitats no és difícil, però com podem fer aquesta suma si en tenim un nombre infinit? En matemàtiques anomenem sèrie a una d’aquestes sumes infinites, i tractar-les porta a resultats molt més sorprenents del que ens podríem imaginar.

La paradoxa de Zenó

Zenó va ser un filòsof grec que va anunciar tot de paradoxes amb l’objectiu de demostrar que el moviment era una simple il·lusió. La més famosa és la de la cursa entre Aquil·les i una tortuga. Com que la tortuga és més lenta, se li deixa avantatge: surt 100m més endavant que Aquil·les. Llavors comença la cursa. Aquil·les correrà fins on era la tortuga, però quan hi arribi, la tortuga haurà avançat uns metres més endavant, per exemple 10m. Així que Aquil·les continuarà corrent fins a la posició on estava la tortuga, 10m més endavant. Quan hi arribi, la tortuga haurà avançat un bocí més i així cada cop. Tal com veiem al dibuix. Arribarà mai Aquil·les a atrapar la tortuga?

La cursa entre Aquil·les i la Tortuga, pas a pas

Podem reformular la paradoxa perquè ens sigui més fàcil tractar-la. Imaginem que volem caminar des d’un punt inicial fins al següent que està a dos metres de distància. Per a fer-ho recorrem primer una meitat en 1s i per tant ens queda un metre. Després fem el mateix i recorrem la meitat de la meitat, mig metre, que a la mateixa velocitat ho fem en mig segon. I així successivament, cada cop recorrent una meitat del que queda. Arribarem mai al punt que estava a dos metres, i sobretot, quant temps necessitarem?  

Zenó deia que necessitarem infinit temps per realitzar el moviment i per això no té sentit que aquest moviment existeixi. Triguem 1s per al primer metre, després 1/2s per la segona part, després 1/4s, etc. Per a Zenó el resultat de sumar infinits nombres és infinit. Però tenia raó?

Què ens diu la intuïció?

En matemàtiques sempre és bo guiar-nos per la nostra intuïció, tot i que l’hem de passar pel dur examen de la lògica per assegurar-nos que és correcta. 

Imaginem que només sumem positius, no restem mai -restar és sumar nombres negatius-. Semblaria que el resultat ha de donar sempre infinit, però això ho podem descartar ràpidament ja que si sumem 0+0+0+0+0+…, és a dir, sumem zero infinites vegades, el resultat serà zero. Bé, em podeu dir que aquest és un exemple estúpid i que qualsevol altra suma infinita donarà infinit, ja que si sempre sumem coses positives, podrem créixer tant com vulguem, com pensava Zenó.

Aquesta idea és errònia i la suma següent ens ho demostra.

La sèrie geomètrica

Volem sumar: u, més un mig, més un quart, més un vuitè, etcètera. Volem sumar tots els inversos de les potències de 2 -és a dir, u dividit entre 2, entre 2^2=4, entre 2^3=8,…

    \[1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots\]

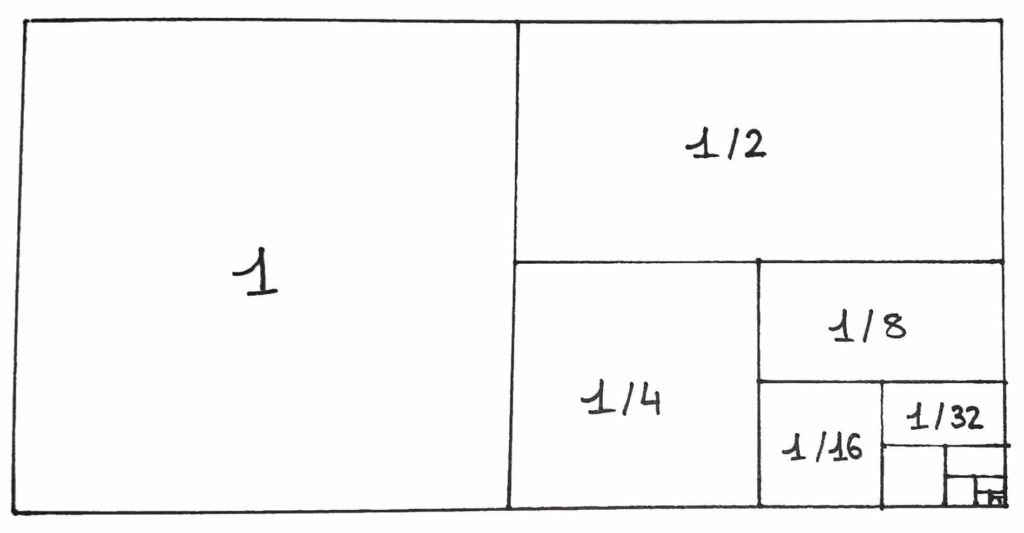
Sumar

i mirar si dona un número, diferent d’infinit. Per a fer-ho, suposem que això passa i anomenem s a aquest número. Per tant,

    \[s=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots\]

Ara, fem un truc matemàtic aparentment estúpid que és multiplicar-ho tot per 2. Al costat esquerra ens quedarà 2s i al dret, per les propietats de la multiplicació, sabem que multiplicar per dos tota la suma és igual que multiplicar per dos cada terme:

    \begin{align*}& 2s=2\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\cdots\right)=\\&=2\cdot1+2\cdot\frac{1}{2}+2\cdot\frac{1}{4}+2\cdot\frac{1}{8}+2\cdot\frac{1}{16}+2\cdot\frac{1}{32}+\cdots=\\&=2+\underbrace{1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots}_s \end{align*}

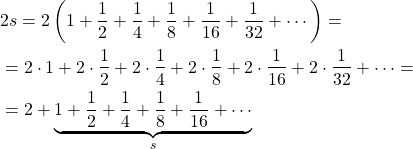
on veiem que al final ens queda que 2s és igual a dos més… la suma inicial! Ens ha tornat a aparèixer. Com que aquesta suma li havíem dit s, la podem canviar tota per s,

    \[2s=2+s\]

Aquesta equació és fàcil resoldre-la si restem s a cada costat de la igualtat:

    \[2s-s=2+s-s\]

per tant,

    \[s=2\]

Sorprenentment, el resultat de sumar infinits termes, en aquest cas no dona infinit, sinó que dona 2!!

Què vol dir això exactament?

Això ens ha de xocar molt! Com pot ser que una suma, que no acaba mai -té infinits termes!- puguem demostrar que és exactament igual a dos? Per entendre-ho, mirem el que s’anomena sumes parcials: anem sumant per parts des de l’inici fins a un punt concret, primer només el primer terme, després els dos primers, després els 3 primers, després els 4 primers, etc. En el nostre exemple els resultats serien: 1, per la primera; 1+1/2=1,5, per la segona; 1+1/2+1/4=1,75, per la tercera; 1,875 per la quarta, etc. Els resultats que ens van sortint cada cop s’acosten més i més a dos, sense passar-lo mai. És a dir, tendeixen a 2. Quan passa això diem que la sèrie convergeix.

Llavors, què vol dir que una suma infinita doni infinit? 

Una suma infinita dona infinit quan les sumes parcials -és a dir, sumar des de l’inici fins a un lloc concret- van creixent sense parar, és a dir, a mida que anem sumant termes la suma va creixent més i més. D’altra forma, que per a qualsevol nombre -per gran que sigui- sempre podem trobar una suma parcial a partir de la qual les següents seran més grans. Vegem-ho amb l’exemple més senzill possible,

    \[1+1+1+1+1+1+1+1+...\]

sembla molt clar que aquesta sèrie suma infinit, però cal demostrar-ho. Aquí les sumes parcials són 1, 2, 3, 4… Si ens imaginem un número gran per exemple el 1002, és clar que si sumem 1+1+…+1 mil tres vegades -que és la suma parcial 1003- haurem passat el valor i totes les següents sumes parcials també ho faran -la següent donaria 1004, després 1005… Això amb qualsevol número que se’ns acudeixi: per gran que sigui, sempre hi haurà un moment que la nostra tira d’uns sumarà més que el número. En aquest cas, la sèrie “suma” infinit.

La intuïció ens falla de nou

Em podeu dir que les dues sèries que us he posat no tenen res a veure, que són completament diferents, que no és estrany que una sumi infinit i l’altra no. A la primera, cada cop sumàvem una cosa més petita i per tant sembla lògic que al final sumem tan poca cosa que no pugui passar d’un valor determinat. Això, però, no és sempre així, mirem ara la sèrie

    \[1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\cdots\]

si ens hi fixem veiem que el primer terme és major que 1/2 -clar! ja que 1>1/2. Igualment amb el segon terme passa clarament. Fixem-nos en el tercer i quart terme. Com que cada un és una mica més petit que l’anterior, podem dir que la suma dels dos és més gran que la suma de dues vegades l’últim:

    \[\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\]

ja que 1/3>1/4 com dèiem. Així el tercer i el quart terme són també majors que 1/2. Ja podeu veure què és el que vull fer. Ara fem el mateix per als següents 4 termes, com abans, el més petit és l’últim,

    \[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}\]

perquè terme a terme 1/5>1/8, 1/6>1/8, etc. I ho podem tornar a fer per als següents 8 termes, els 16 de després, els 32, etc. Cada bloc serà major que 1/2, penseu-hi un moment si cal. És a dir, 

    \begin{align*} &1+\frac{1}{2}+\left[\frac{1}{3}+\frac{1}{4}\right]+\left[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right]+\cdots\geq\\ \geq&\frac{1}{2}+\frac{1}{2}+\left[\frac{1}{4}+\frac{1}{4}\right]+\left[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right]+\cdots=\\=&\frac{1}{2}+\frac{1}{2}+\quad\quad\,\frac{1}{2}+\quad\quad\quad\quad\quad\quad\quad\frac{1}{2}+\cdots \end{align*}

si agafem prou termes. O sigui, la nostra sèrie és més gran que una sèrie d’anar sumant 1/2. Com que aquesta donarà infinit de forma semblant al que hem vist abans amb la d’uns, la nostra també ho ha de fer, ja que ha de donar un resultat més gran! És a dir, encara que sumem cada cop coses més petites pot ser que la suma total ens doni infinit.

Resolem la paradoxa

Des d’un punt de vista matemàtic, sembla que la seva paradoxa està resolta, ja que el temps no suma infinit, en Zenó s’equivocava! Si sumem tot el temps que hem gastat (1+1/2+1/4+1/8+…) obtenim la suma geomètrica que estudiàvem a l’inici, que dona 2 segons. Per tant, en un nombre infinit de passes haurem arribat al punt final, però en un nombre finit de temps.

Sembla que en fer aquest recorregut estem completant un procés infinit. Però un procés infinit no té un últim pas -ja que és infinit! Llavors, com pot ser que l’acabem? Aquest tema ha preocupat molts dels grans filòsofs, matemàtics i físics dels últims 2000 anys.

Ja per acabar…

Les sèries infinites es poden anar complicant més i més. Per exemple en considerar els negatius, passen coses més estranyes, algunes sèries no acaben sumant ni un nombre fix ni infinit, sinó que van saltant entre dos valors. Fins i tot hi ha sèries que convergeixen a un nombre, però reordenant els seus termes podem fer que sumin el resultat que vulguem.  Aquest resultat va ser demostrat pel matemàtic alemany Riemann.

Georg Friedrich Bernhard Riemann

També en sèries de nombres positius passen coses curioses com aquesta:

    \[1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+\cdots=\frac{\pi^2}{6}\]

Com pot ser que aparegui el nombre pi -que té a veure amb cercles- en aquesta suma infinita? Poder trobar aquest tipus de relacions entre coses aparentment allunyades és una de les parts més interessants i divertides de les matemàtiques. Podeu trobar una demostració geomètrica – i molt elegant i visual- d’aquest resultat al primer enllaç de l’apartat Per a saber-ne més (en anglès).

Per a saber-ne més

3Blue1Brown – Why is pi here? And why is it squared? A geometric answer to the Basel problem

TED-ed – What is Zeno’s Dichotomy Paradox? – Colm Kelleher

Viquipèdia – Sèrie geomètrica